R. Grothmann
Wir wollen die Kettenlinie bestimmen, und zwar durch eine Messung und durch die Lösung einer Differentialgleichung. Außerdem soll die Messung mit dem theoretisch erwarteten Ergebnis verglichen werden.
Zuerst lesen wir die Daten einer gemessene Kette ein. Die Kette wurde vor den Bildschirm geklebt und mit der Funktion mouse() wurden die Bildpunkte abgenommen.
>P=getmatrix(24,2,"kette.dat")';
Wir geben die Messpunkte und die verbundene Kurve aus.
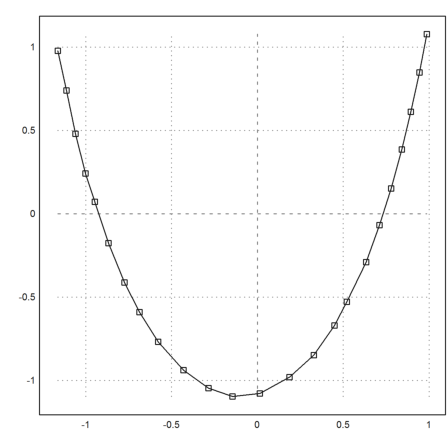
>plot2d(P[1],P[2]); ... plot2d(P[1],P[2],add=1,points=1,style="[]"):
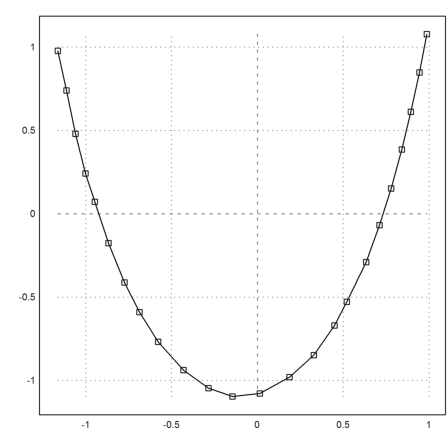
Versuchen wir zunächst, eine Parabel mit diesen Punkten in Übereinstimmung zu bringen.
>p=polyfit(P[1],P[2],2)
[-1.15889, 0.356736, 1.8091]
>y=polyval(p,P[1]); ... plot2d(P[1],y,color=10,add=1):
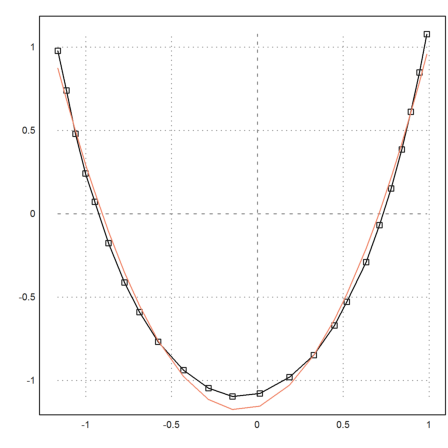
Die Zeichnung zeigt, daß die Übereinstimmung nicht groß ist. Galileo täuschte sich, als er glaubte, die Kettenlinie sei die Parabel.
Versuchen wir es mit einer physikalischen Überlegung und einer aus kleinen Teilen zusammengesetzten Kette.
Die Zugkraft der Kette ist der Kraftvektor, der in jedem Punkt nach unten zieht. Wir überlegen uns, dass die y-Kompente der Zugkraft in der Kette im festen Verhältnis mit der Kettenlänge zunimmt, da ja das Gewicht des Kettenstücks von da an nach unten zieht. Die x-Komponente der Zugkraft bleibt immer gleich.
![]()
Wenn man die Kette aus gleich großen Kettengliedern zusammensetzt, so muss y-Komponente der Kraft also kontinuierlich zunehmen, und die x-Komponente gleich bleiben.
>ky=-1:0.01:1; kx=ones(size(ky));
Die Kette geht in Richtung der Kraft und setzt sich aus lauter kleinen gleich langen Teilstücken zusammen. Wir normieren daher die Kraftkomponenten und erhalten die Richtungen der Stücke.
>ds=sqrt(kx*kx+ky*ky)*100;
Aufsummieren ergibt die Kette.
>X=0|cumsum(kx/ds); Y=0|cumsum(ky/ds);
Wir normieren noch so, daß die Kette im Ursprung am tiefsten hängt, und symmetrisch zu 0 liegt.
>X=X-(X[1]+X[cols(X)])/2; Y=Y-min(Y); ... plot2d(X,Y):
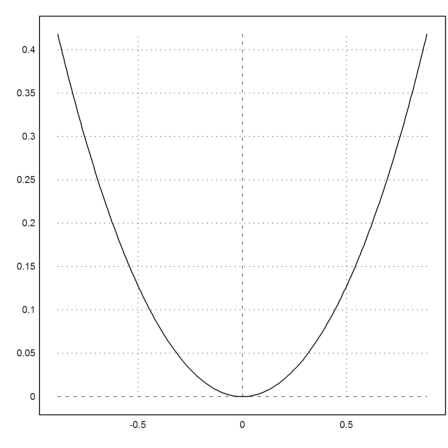
Es ist nicht einfach einzusehen, warum eine Linie der obigen Form im Grenzwert eine eine cosh-Funktion ergibt. Dazu lese man bitte im Internet nach.
Wir bestimmen eine cosh-Kurve, die die obige Kurve interpoliert, und zeichnen den Fehler.
>a=bisect("x*cosh(X[1]/x)-x-Y[1]",1,1000)
1.00002390404
>y1=a*cosh(X/a)-a; max(abs(Y-y1))
1.24997272464e-005
Wie man sieht, ist der Fehler verschwindend gering.
Versuchen wir nun, eine Funktion vom Typ
![]()
an die gemessene Funktion anzupassen. Der Faktor a/c ist der Verzerrungsfaktor des Bildschirms bei der Messung.
Zunächst wird die Funktion jedoch neu gezeichnet.
>plot2d(P[1],P[2]); ... plot2d(P[1],P[2],add=1,points=1,style="[]"):
Anschließend programmiert man die zu minimierende Funktion.
>function f(x) ... global P; y=x[1]*cosh((P[1]-x[2])/x[3])-x[4]; return sum((y-P[2])^2); endfunction
Das Minimum wird mit der Methode von Nelder berechnet.
>x=neldermin("f",[1,1,1,1])
[0.649219, -0.0971185, 0.505737, 1.73762]
Dies ergibt eine zufriedenstellende Übereinstimmung.
>plot2d(P[1],x[1]*cosh((P[1]-x[2])/x[3])-x[4],add=1,color=10):
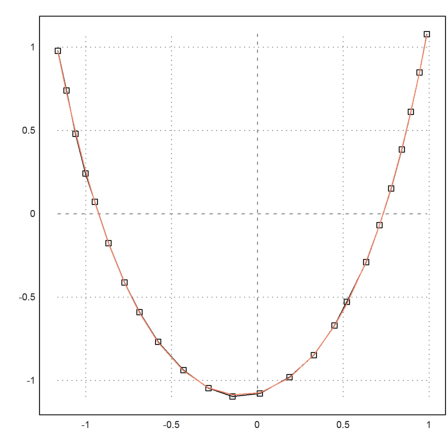
Im Folgenden versuchen wir, eine Kette bestimmter Länge zwischen zwei Punkten aufzuhängen.
Zunächst die Funktion für eine Kettenlinie
![]()
mit Parametern a,b,c.
>function k (x,a,b,c) ... return a*(cosh((x-b)/a))-c endfunction
Ein Test.
>plot2d("k",-1,1;1,0,1):
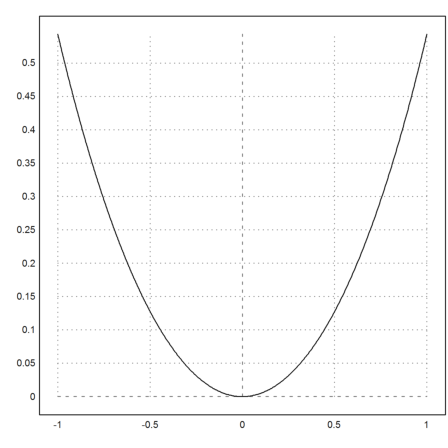
Nun das Längenelment
![]()
dieser Funktion, das wir mit Maxima berechnen und direkt in die Funktion kd einsetzen.
>function kd (x,a,b,c) ... return @:"sqrt(1+diff(a*cosh((x-b)/a),x)^2)" endfunction
Mit dem Gauß-Integrator berechnen wir die Länge der obigen Kettenlinie.
>gauss("kd",-1,1;1,0,1)
2.35040238729
Daraus machen wir eine Funktion.
>function kl (x1,x2,a,b,c) ...
return gauss("kd",x1,x2;a,b,c)
endfunction
Gelöst werden müssen nun die Interpolationsbedingungen
![]()
sowie die Längenbedingung
![]()
Wir wollen das Nelder-Mead Verfahren verwenden und schreiben daher eine Funktion mit dem Minimum in der Lösung.
>function res (v,x1,y1,x2,y2,length) ... return (k(x1,v[1],v[2],v[3])-y1)^2 .. + (k(x2,v[1],v[2],v[3])-y2)^2 .. + (kl(x1,x2,v[1],v[2],v[3])-length)^2 endfunction
Ein Test.
>v=neldermin("res",[1,0,0];-1,0.8,1,0.5,3)
[0.620621, 0.0622702, 0.974518]
Sieht gut aus!
>plot2d("k",-1,1;v[1],v[2],v[3]):
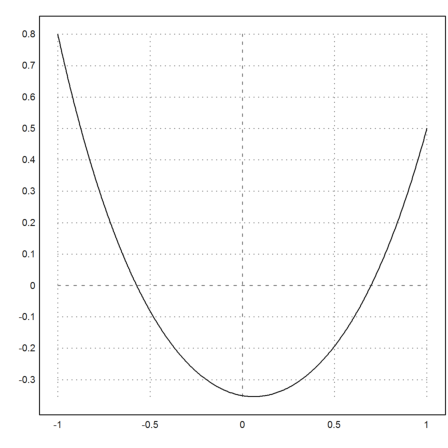
Und die Länge stimmt.
>kl(-1,1,v[1],v[2],v[3])
2.99999991995
Die folgende Funktion wartet auf zwei Mausklicks und berechnet die Kette dazwischen.
>function test (length) ...
setplot(-1,1,-1,1); clg; xplot(); title("Zwei Mausklicks!");
m1=mouse(); hold on; mark(m1[1],m1[2]); hold off;
m2=mouse(); hold on; mark(m2[1],m2[2]); hold off;
setplot();
v=neldermin("res",[1,0,0];m1[1],m1[2],m2[1],m2[2],length);
t=linspace(m1[1],m2[1],300); s=map("k",t;v[1],v[2],v[3]);
plot2d(t,s,a=-1,b=1,c=-1,d=1);
plot2d([m1[1],m2[1]],[m1[2],m2[2]],points=1,add=1);
return v
endfunction
>v=test(3); // Klicken Sie! >insimg;